השפעת שדות מגנטים על מעגלי תהודה מוליכי על

מעגלי תהודה מבוססי מוליכי על, משמשים למגוון אפליקציות, לדוגמה – גלאי השראות קינטית , Circuit quantum electrodynamics, Qubits וכו'. עמידותם של מעגלי התהודה לשדות מגנטים חשובה לביצועים יציבים ועקביים בסביבה של שדות מגנטים. למעגלי תהודה אלו, ישנו רכיב השראות הנקרא 'השראות קינטית' שתלוי בצפיפות נושאי המטען במוליך על – זוגות הקופר. כתוצאה מכך, תדר התהודה (וה-Q-factor), תלויים בצפיפות זוגות הקופר אשר בתורם תלויים בשדה מגנטי, זרם, פוטונים וטמפרטורה. במאמרים [1], [2], [3] שבוצעו על מעגלי תהודה בעלי רוחב פסים של 10 מיקרון במגוון חומרים שונים, הראנו לראשונה כי ההשפעה של שדות מגנטים מושפעות מכמה מנגנוני מוליכי על שונים. כאשר מפעילים את השדה המגנטי אחרי שמעגל התהודה מקורר לטמפרטורה הקריטית ישנה ירידה חדה בתדר התהודה כתוצאה מקיומם של זרמי מיסוך. הירידה החדה של תדר התהודה נגמרת לאחר שזרמי המיסוך חודרים לכל רוחב הדגם. לאחר מכן, ההתנהגות מושפעת מקיומם של 'וורטקסים מגנטים' הגורמת להתנהגות הלינארית. התנהגות לינארית זו תלויה גם כן בשדה הקריטי של מוליך על. תופעת ההיסטריז (תדר התהודה אינו חוזר לערכו הראשוני) נגרמת ומוסברת גם כן באמצעות זרמי מיסוך ו-וורטקסים מגנטים.

כתוצאה מההבנות הנ"ל, ייצרנו מעגלי תהודה בעלי רוחב פס של 200 ננומטר מבוססי NbN [4]. רוחב זה נבחר מתוך הבנה שרדיוסם של הוורטקסים המוגדר לפי λL, עומק החדירה של לונדון, גדול מרוחב הפס ולא הם לא יחדרו לדגם. נוסף על כך, גם זרמי המיסוך מתנהגים אחרת ברוחב פס שכזה. ואכן, התוצאות הראו שתדר התהודה מתנהג בדומה לתאוריה שבה חודר שדה מגנטי שאינו מקוונטט לדגם, ואכן אין היסטריז.

תמונה ממיקרוסקופ אלקטרונים סורק (SEM) של מעגל תהודה מבוסס NbN בעל רוחב חוטים של 200 ננומטר. האזורים הלבנים והשחורים מייצגים את מוליך העל ואת המצע החשוף, בהתאמה.

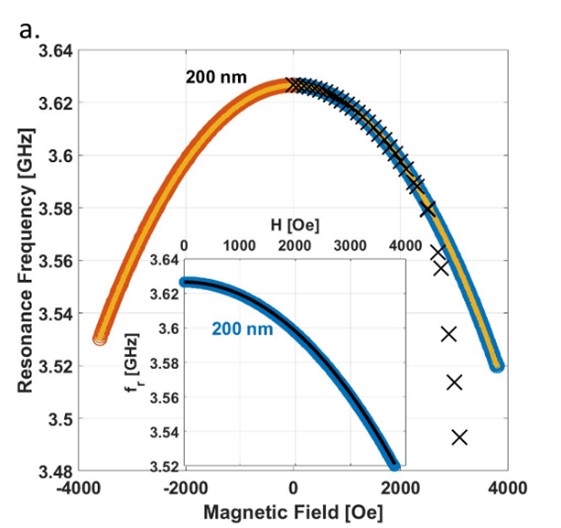
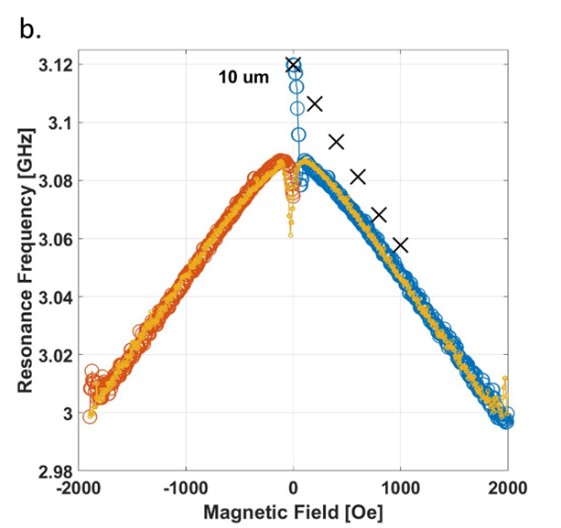
תלות תדר התהודה, fr, בשדה מגנטי ב-2.1 קלווין עבור (a) מעגל התהודה ברוחב 200 ננומטר ו-(ב) מעגל התהודה ברוחב  10 מיקרומטר. במדידות ZFC (קירור בשדה אפס), השדה הוגבר מאפס ל-4000 Oe (עיגולים כחולים). לאחר מכן הוא הורד ל-4000 Oe (צהוב) וחזרה לאפס (אדום). ניתן לראות את התלות השונה בין מעגלי התהודה, כתוצאה מכך שאופן חדירת השדה המגנטי שונה בין הדגמים.

[1]        A. Roitman, A. Shaulov, and Y. Yeshurun, “Characterization of YBa2Cu3O7-δ  coplanar resonator for microwave kinetic inductance detectors,” Supercond. Sci. Technol., vol. 36, no. 1, p. 015002, Jan. 2023, doi: 10.1088/1361-6668/ac9eea.

[2]        A. Roitman, A. Shaulov, and Y. Yeshurun, “Effect of Magnetic Fields on Superconducting Microwave Coplanar Resonators,” IEEE Trans. Appl. Supercond., vol. 33, no. 5, pp. 1–4, Aug. 2023, doi: 10.1109/TASC.2023.3247979.

[3]        A. Roitman, C. Pfaff, T. Hauet, A. Shaulov, and Y. Yeshurun, “Microwave Kinetic Inductance Detector Made of Molecular Beam Epitaxy (MBE)-Grown MgB2 Film,” Nanomaterials, vol. 14, no. 21, p. 1731, Oct. 2024, doi: 10.3390/nano14211731.

[4]        A. Roitman, L. Burlachkov, A. Sharoni, A. Shaulov, and Y. Yeshurun, “Suppression of magnetic vortex losses in submicron NbN coplanar waveguide resonators,” Sci. Rep., vol. 14, no. 1, p. 26444, Nov. 2024, doi: 10.1038/s41598-024-76166-7.