The Effect of Magnetic Fields on Superconducting Resonators

Superconducting resonant circuits are used in a variety of applications, such as kinetic inductance detectors, circuit quantum electrodynamics, qubits, and more. The resilience of these resonant circuits to magnetic fields is crucial for stable and consistent performance in magnetically active environments. These resonant circuits include an inductive component known as kinetic inductance, which depends on the charge carrier density in the superconductor—specifically, Cooper pairs. As a result, the resonance frequency (and the Q-factor) is influenced by the Cooper pair density, which in turn is affected by magnetic fields, currents, photons, and temperature. In studies [1], [2], [3] conducted on resonant circuits with a strip width of 10 microns across various materials, we demonstrated for the first time that the influence of magnetic fields is governed by multiple superconducting mechanisms. When a magnetic field is applied after the resonator has been cooled below its critical temperature, there is a sharp drop in the resonance frequency due to the presence of screening currents. This sharp decrease in resonance frequency ceases once the screening currents penetrate the entire width of the sample. Subsequently, the system's behavior is influenced by the presence of magnetic vortices, leading to a linear dependence. This linear behavior is also governed by the superconductor's critical field. The phenomenon of hysteresis (where the resonance frequency does not return to its initial value) is also explained by the effects of screening currents and magnetic vortices.

Based on these insights, we fabricated NbN-based resonant circuits with a strip width of 200 nanometers [4]. This width was chosen based on the understanding that the vortex radius, defined by the London penetration depth (λL), is larger than the strip width, preventing vortex penetration into the structure. Additionally, screening currents behave differently in such narrow strips. Indeed, our results showed that the resonance frequency follows the theoretical prediction for a system where a non-quantized magnetic field penetrates the sample, and no hysteresis is observed.

SEM picture of the 200 nm strips resonator based on NbN. White and black regions present the superconductor and the bare substrate, respectively.

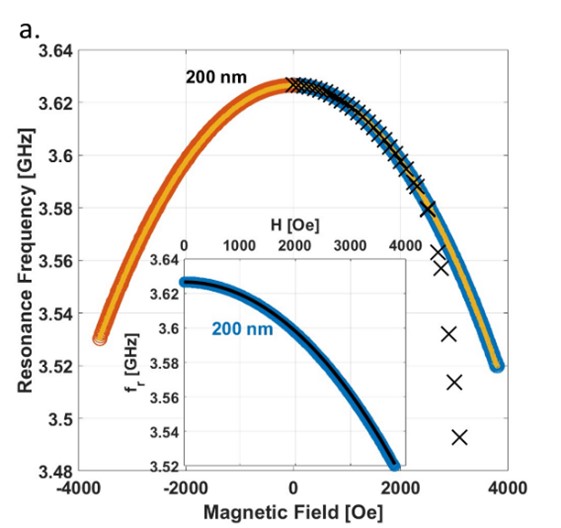
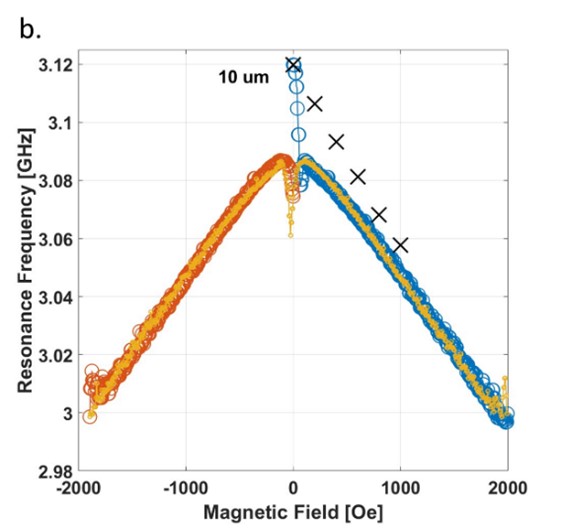
Figure 4. Magnetic field dependence of the resonance frequency, _fr, at 2.1 K for (a) the 200 nm and (b) the 10 μm resonators. In ZFC measurements, the field was ramped up from zero to 4000 Oe (blue circles).  It was then ramped down to -4000 Oe (yellow) and back to zero (red). The different dependencies between the resonators can be seen, as a result of the different ways in which the magnetic field penetrates the samples.

[1]        A. Roitman, A. Shaulov, and Y. Yeshurun, “Characterization of YBa2Cu3O7-δ  coplanar resonator for microwave kinetic inductance detectors,” Supercond. Sci. Technol., vol. 36, no. 1, p. 015002, Jan. 2023, doi: 10.1088/1361-6668/ac9eea.

[2]        A. Roitman, A. Shaulov, and Y. Yeshurun, “Effect of Magnetic Fields on Superconducting Microwave Coplanar Resonators,” IEEE Trans. Appl. Supercond., vol. 33, no. 5, pp. 1–4, Aug. 2023, doi: 10.1109/TASC.2023.3247979.

[3]        A. Roitman, C. Pfaff, T. Hauet, A. Shaulov, and Y. Yeshurun, “Microwave Kinetic Inductance Detector Made of Molecular Beam Epitaxy (MBE)-Grown MgB2 Film,” Nanomaterials, vol. 14, no. 21, p. 1731, Oct. 2024, doi: 10.3390/nano14211731.

[4]        A. Roitman, L. Burlachkov, A. Sharoni, A. Shaulov, and Y. Yeshurun, “Suppression of magnetic vortex losses in submicron NbN coplanar waveguide resonators,” Sci. Rep., vol. 14, no. 1, p. 26444, Nov. 2024, doi: 10.1038/s41598-024-76166-7.